Hoe bouw je iets ronds met LEGO steentjes?
Hoe bouw je vormen met vierkante LEGO-steentjes, welke rekentechnieken komen daarbij kijken en welke rol speelt Minecraft hierbij??

Ronde vormen van vierkante stenen
LEGO is geen medium dat geschikt is voor het bouwen ronde vormen. Het basisbouwblok – een 1×1-steen – heeft immers een vierkante voetafdruk, een LEGO-bodemplaat heeft die een regelmatig vierkant raster geplaatst.
En toch zijn er veel prachtige LEGO-creaties die ronde vormen bevatten – allerlei soorten cilinders en zelfs bollen.
Wij hadden veel ervaring met het bouwen van deze vormen met LEGO totdat wij begonnen met het werken aan onze eigen versie van de Taj Mahal. Het middelpunt van dit beroemde monument, dat toevallig een van de moderne wereldwonder is, is de enorme koepel die op een cilindervormige basis staat, welke de trommel wordt genoemd (dit is een echte architectonische term). De mintten die op de vier hoeken van de sokkel de Taj Mahal staan, zijn feite ook gestapelde cilinders.


Enige tijd geleden stuitten we op het model van de Taj Mahal, vervaardigd de overleden Arthur Gugick. Dit opmerkelijke model ging vooraf aan de LEGO Creator Expert 10189-set en diende als het centrale rekwisiet in de onafhankelijke Australische film genaamd "Taj" (de plot draait vader die weer contact maakt met zijn vervreemde dochter door samen met haar een LEGO-model van de Taj Mahal te bouwen).
We wisten meteen dat we onze eigen van de Taj Mahal wilden maken, we er niet klaar voor. We moesten nog veel leren voordat we recht konden doen aan dit wereld.r.
Hoe indrukwekkend Sean Kenney's model van het Empire State Building ook was, we hadden niet veel moeite om intuïtief te begrijpen hoe het was gebouwd. Een wolkenkrabber zoals het State Building is in feite een stapel verdiepingen: je hoeft alleen maar een paar varianten van het vloerontwerp te maken en deze zo vaak te herhalen als nodig is om het geheel te construeren. Het wordt interessanter wanneer je de top van een klassieke wolkenkrabber bouwt (waar deze taps toeloopt naar een torenspits), maar je geconfronteerd metische (met opvallende uitzonderingen, zoals de kroon van het Chrysler Building).
De Taj Mahal daarentegen bevat verschillende organische vormen – bogenare en natuurlijk koels – en ik wist helemaal niets over bouwen van ronde vormen LEGO

In de jaren die volgden, terwijl we ons verdiepten in het bouwen van verschillende modellen van wolkenkrabbers, hadden we de Taj Mahal altijd in ons achterhoofd.
Sterker nog, we zijn meer eens begonnen aan een model van de Taj Mahal voordat we het opgaven omdat we simpelweg konden achterhalen hoe we een boog of een ander element in het model moesten maken.
We moesten bovendien grondige verkenning maken van alle technieken die er zijn om ronde vormen te creëren met LEGO; we hebben in het internet afgespeurd naar alle informatie die we dit onderwerp konden vinden. Bij elke stap waren we verbaasd en geïnspireerd door de eindeloze creativiteit van de AFOL-community, we hebben ook enkele tools gebruikt die door de Minecraft-community zijn ontwikkeld.

In wat waarschijnlijk een bewijs is van onze groei als bouwers, slaagden we erin om het ontwerp van de Taj Mahal deze keer soepel door te lopen. We maakten gebruik van alle technieken die we hadden geleerd bij het van wolkenkrabbermodellen - SNOT, halve stud offsets, schuine muren, enzovoort - evenals enkele nieuwe technieken die we uit ons onderzoek hadden opgepikt.
Wij hopen dat dit artikel enige helderheid kan bieden over fascinerende onderwerp van het bouwen van ronde vormen met LEGO. Wij kunnen niet beweren dat wij een van de technieken hebben uitgevonden die in dit artikel worden genoemd, maar wij catalogiseren ze graag hier voor toekomstige referentie (waar mogelijk met vermelding van de uitvinders).
De cirkel vierkant maken
Wat houdt het maken van ronde vormen van LEGO precies in? De titel van dit bericht verwijst naar "het vierkant maken van de cirkel", een eeuwenoud wiskundig probleem dat mensen eeuwenlang hebben geprobeerd op te lossen, totdat in 1882 werd bewezen dat het onmogelijk is om dit probleem op te lossen. Het is echter mogelijk om dichtbij genoeg te komen door een benadering van het getal π (pi) te gebruiken.
Op vrijwel dezelfde manier proberen alle hier beschreven technieken vierkante of rechthoekige stenen of platen gebruiken om de best mogelijke benadering van de ronde vorm te creëren.
Het resultaat is nooit perfect en de beperkingen van het LEGO-medium zijn altijd zichtbaar in de grilligheid van de rondingen en de gaten die men kan zien, vooral wanneer men het model van dichtbij bekijkt. De kunst is echter om een redelijk overtuigende illusie van een ronde vorm te creëren, althans wanneer men het model van een afstand bekijkt.
1) SNOT gebruiken om kleine cilinders te maken
Voor de minaretten van de Taj Mahal wilden we niet beperkt worden door de kleine selectie cilinderstukken die LEGO heeft. We wilden een andere manier proberen om cilinders te bouwen die geschaald konden worden naar elke gewenste hoogte. We waren al bekend met het gebruik van gebogen hellingen en SNOT om ronde vormen te creëren (we hadden deze techniek gebruikt om de kroon te bouwen in ons model van het Chrysler Building). Dezelfde techniek kan worden gebruikt om cilinders met verschillende diameters te maken. Alle cilinders op de onderstaande afbeelding kunnen worden gebouwd in hoogte-intervallen van twee studss.

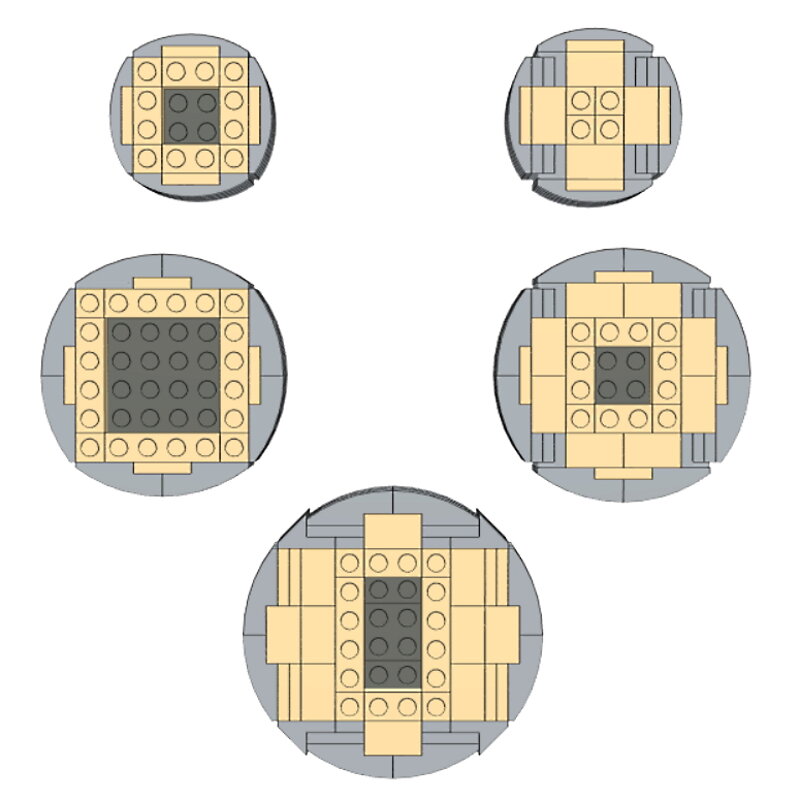
De kleinste cilinder was precies goed voor de minaretten van de Taj Mahal op basis van de schaal die ik gebruikte. Idealiter zouden de minaretten taps toelopen naarmate ze stijgen – zoals ze dat doen in de echte Taj Mahal. Helaas was er geen eenvoudige manier om de diameter van de kleinste cilinder verder te verkleinen.
2) LEGO-muren buigen om ronde vormen te creëren
Een "brute" methode om ronde muren te construeren met LEGO is door rechte muren te bouwen en deze vervolgens te buigen om een cirkel te vormen. Hoe langer de muur, hoe meer flexibil deze zal bezitten, waardoor het eenvoud wordt om deze in een volledige cirkel te buigen. Het aantal 12 stenen dat in elke laag nodig is voor eeniele ronde muur ligt doorgaans rond de 72, plus of min enkele stenen. Er zijn echter bekend waarin ronde muren gebouwd met aanzienlijk minder platen per laag.
Bekijk het werk van Jeff Sanders die gespecialiseerd is in "brick bending". Hij heeft een indrukwekkend portfolio van creaties, gemaakt door LEGO stenen muren niet alleen in cirkels te buigen, maar ook in verschillende andere vormen.
Houd er rekening mee dat de meeste baksteenbuigtechnieken strikt genomen "illegaal" zijn, omdat je LEGO elementen gebruikt op manieren waarvoor ze niet bedoeld zijn en ze blootstelt aan onnodige spanning en mogelijke schade. Een duidelijk nadeel van deze techniek (behalve dat het illegaal is) is het feit dat het niet digitaal kan worden gerepliceerd in de Stud.io software van BrickLink.
Een paar jaar geleden begonnen we aan een LEGO-project dat anders was dan alle andere waar we ooit aan hadden gewerkt. We wilden een ronde vorm maken van een mozaïek met studs-up. We bedachten ons eigen patroon van in elkaar verstrengelde slangen en gebruikte iets meer dan 14.000 platen om dit ronde ding te bouwen dat we graag zie als een soort vaas (omdat een prullenbak niet zo aantrekkelijk is). Dit staat ergens in een hoekje in onze kelder, omdat we nog steeds geen goede manier heb gevonden om dit af te maken en iets te maken dat het waard is om te laten zien. Suggesties zijn natuurlijk welkom!
3) Mengen van gewone stenen met ronde 1×1 stenen
Deze techniek gebruikt dezelfde aanpak als hierboven – behalve dat we 1×1 ronde stenen (of platen) in onze muur gebruiken om deze gemakkelijker (en legaal!) te kunnen buigen. Als we 1×3 stenen in onze muur afwisselen (1×2 stenen werken ook) met 1×1 ronde stenen, werken de ronde stenen tot op zekere hoogte als scharnieren, waardoor de muur kan worden gebogen om een cirkel te vormen. Met deze methode kunnen ronde muren worden gebouwd met kleinere diameters dan mogelijk is met de vorige methode.
Het enige nadeel is dat de textuur van de muur ongelijk is vanwege de 1×1 ronde stenen. Het is mogelijk om tegels te gebruiken om de ronde stenen te verbergen en het effect van een echte bakstenen muur te creëren (credits gaan naar Steve DeCraemer op Flickr). De 1×3 stenen worden hier vervangen door 3 koplampstenen met hun bovenste noppen naar buiten gericht. Deze koplampstenen worden met 1×3 platen aan elkaar verbonden, terwijl 1×4 tegels aan de voorkant van de ronde muur worden bevestigd, waardoor het lijkt op een bakstenen muur (wat geweldig zal werken bij het bouwen van kastelen).
4) Ronde muren met behulp van scharnierstenen en platen
We hebben gezien dat scharnierstukken erg handig kunnen zijn voor het maken van hoekige muren en verschillende veelhoeken (zeshoeken, achthoeken, enz.). Hoe groter het aantal zijden in een regelmatige veelhoek (een waarbij alle zijden dezelfde lengte hebben), hoe dichter het bij een cirkel komt. We kunnen dit feit gebruiken om scharnierstukken te gebruiken om ronde muren te maken.
Een tutorial die ik over dit onderwerp tegenkwam, was van Eggy Pop op Flickr. Ik heb de ronde muur die in deze tutorial wordt getoond, opnieuw gemaakt in Stud.io met behulp van 14 1×4 scharnierplaten om de cirkel te voltooien (wat in feite een veelhoek is met 28 twee-stud brede zijden). Een van de leuke dingen aan deze specifieke ronde muur is dat de diameter (18 studs aan de binnenkant, 20 studs aan de buitenkant) een geheel getal is in termen van studs. Zoals je kunt zien, liggen de scharnierplaten aan 4 zijden op één lijn met het LEGO-raster, waardoor de ronde muur stevig aan een basis kan worden bevestigd.
Dus wat is er speciaal aan het getal 18? Laten we eens kijken of we wat wiskunde kunnen gebruiken om dat uit te rekenen. Ervan uitgaande dat de binnenkant van de muur dicht genoeg bij een cirkel ligt, zou de omtrek de diameter keer π (pi) = 18 x 3,14 = 56,52 studs zijn. Deel dat nu door 4 (de lengte van een 1×4 scharnierplaat) en je krijgt 14,13, wat dicht genoeg (voor praktische doeleinden) bij een geheel getal 14 ligt – wat toevallig het aantal scharnierplaten is dat we hebben gebruikt.
Reken er niet op dat hetzelfde werkt voor ronde muren met binnendiameters van bijvoorbeeld 17 of 19 studs. Welke andere getallen werken? De twee getallen die het dichtst bij 18 liggen en werken, zijn 14 en 23 (ik gebruikte 23 voor de trommel in mijn Taj Mahal). Zoals je op de foto's kunt zien, werken deze twee getallen niet zo goed als 18 en de scharnierplaten aan slechts 2 kanten komen overeen met het LEGO-raster (wat meestal goed genoeg is).
Kunnen we uitleggen waarom? In het geval van 14 is het aantal benodigde scharnierplaten (14 x 3,14) / 4, wat ongeveer 11 is. Omdat het aantal scharnierplaten geen even getal is, komen de scharnierplaten niet aan alle 4 de kanten overeen met het LEGO-raster. In het geval van 23 is de diameter zelf niet even. Als u de scharnierplaten op één as uitlijnt met het rooster, wordt de andere as met een halve balk verschoven (indien nodig kunt u jumperplaten gebruiken om de ronde wand aan de basis aan de andere twee zijden te bevestigen).
Voor nu heb ik gewoon een gewone binnenmuur gebouwd die zo dicht mogelijk bij de ronde muur ligt en kaashellingen, gebogen hellingen, enz. aan de binnenmuur bevestigd met behulp van SNOT om de gaten zo goed mogelijk op te vullen. Omdat de trommel een buitendiameter heeft van 25 noppen en ik hem moest centreren op een 24×24 basis, heb ik uiteindelijk jumperplaten gebruikt. Ik had ook jumperplaten nodig om de koepel (die is gebouwd met een kern van 16×16 noppen) op de bovenkant van de trommel te centreren.
Hoewel het vrij eenvoudig is om deze ronde muren te bouwen met echte stukken, hoe doe je dat in Stud.io? Met de scharniertool kun je een stuk selecteren en het rond een scharnierpunt draaien. In dit geval zou het geselecteerde stuk de helft zijn van de 1×4 scharnierplaat. Wanneer je op het stuk klikt met de scharniertool ingeschakeld, zie je eerst een blauwe pijl. Je kunt op deze blauwe pijl klikken en deze slepen om het stuk handmatig te draaien. Of je kunt op de blauwe pijl klikken om een wit tekstvak te krijgen waarin je de precieze hoek kunt invoeren om het stuk te draaien.
Bij ronde muren is het belangrijk om ervoor te zorgen dat alle scharnierplaten precies de juiste hoeveelheid worden gedraaid, anders komen de twee uiteinden van de muur niet goed op één lijn te liggen, zodat u de cirkel kunt voltooien. Om de juiste hoek te bepalen, deelt u 360 door het aantal zijden van de veelhoek die u bouwt. In het geval van de eerste cirkel (diameter 18 noppen) is dit het aantal scharnierplaten maal 2 = 14 x 2 = 28. 360 gedeeld door 28 is 12,85 graden, wat het getal is dat u in het tekstvak moet invoeren. Ik pas deze rotatie meestal toe op één scharnierplaat en kopieer en plak vervolgens de scharnierconstructie (beide helften samen) zo vaak als ik nodig heb.
5) Bollen bouwen door gewone stenen of platen te stapelen
Om te begrijpen hoe bollen worden gebouwd met LEGO-stenen, vond ik het handig om eerst naar de wereld van Minecraft te kijken. Er zijn enkele overeenkomsten tussen Minecraft en LEGO, omdat beide bouwstenen gebruiken met vierkante voetafdrukken die op een vierkant raster worden geplaatst. Een belangrijk verschil is dat de blokken in Minecraft perfecte kubussen zijn, terwijl een eenvoudige 1×1 LEGO-steen dat niet is (hij is hoger dan breed). Daarover later meer. Hoe dan ook, er zijn een aantal bronnen beschikbaar in de Minecraft-community voor het bouwen van bollen en andere vormen met Minecraft-blokken, en ik vroeg me af of ik er een aantal kon gebruiken voor het bouwen van LEGO-bollen.
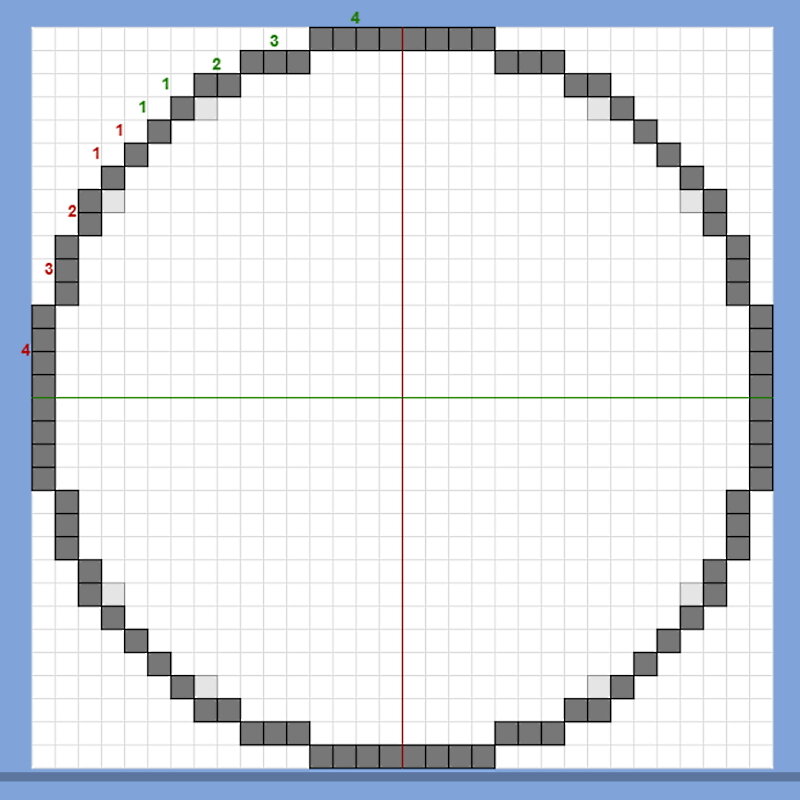
Voordat we naar een 3-dimensionale bol kijken, laten we eens kijken naar een eenvoudige cirkel in 2 dimensies. Minecraft-enthousiastelingen gebruiken vaak wat bekend staat als een cirkeldiagram. Het toont de plaatsing van blokken (of pixels) in een vierkant raster dat het beste een cirkel benadert. Het diagram toont cirkels met verschillende diameters en zoals je op het diagram kunt zien, hoe groter de diameter, hoe overtuigender de illusie van de ronde vorm is.

Minecraft cirkeldiagram
In de Minecraft-wereld waar de bouwstenen perfecte kubussen zijn, kun je ook naar een van de cirkels kijken en het zien als de zijkant van een bol. Je kunt elke rij in het diagram zien als een van de lagen blokken in de bol die je bouwt. Je zou dus in feite beginnen met een laag blokken in een cirkel met de diameter van de bol die je wilt bouwen (dat zou de grootste cirkel zijn die je nodig hebt). Je zou dan lagen stapelen met steeds kleinere cirkels (naarmate je omhoog gaat) totdat je de kleinste cirkel bereikt die je nodig hebt. Herhaal hetzelfde aan de onderkant (waarbij de cirkels kleiner worden naarmate je omlaag gaat) en je hebt een complete bol.
Het kan natuurlijk veel werk zijn om dit allemaal met de hand uit te zoeken (zelfs met behulp van een cirkeldiagram). Gelukkig kan een online tool (Plotz Sphere Generator) dit proces voor je automatiseren. U hoeft alleen maar de gewenste diameter in te voeren en voilà, er wordt een bol voor u gegenereerd (met 3D- en 2D-weergaven die laten zien hoe de bol laag voor laag wordt opgebouwd).

Dat klinkt eenvoudig, toch? Helaas is er veel meer werk bij betrokken als je deze bol wilt bouwen met LEGO-stenen. Ten eerste toont de bolgenerator alleen blokken die gelijk zijn aan 1×1 LEGO-stenen, maar je weet dat deze stenen gewoon niet kunnen worden gestapeld zoals je in de 3D-weergave ziet. Je moet de 1x1's omzetten in langere stenen die een in elkaar grijpende structuur vormen die goed bij elkaar blijft.
Je moet de wanden van de bol ook minstens 2 noppen diep maken, zodat elke opeenvolgende laag (die een kleinere cirkel is naarmate je verder weggaat van de middelste laag) op de laag er direct onder kan rusten. Er is nog één laatste probleem: als je alle blokken in de Minecraft-bol vervangt door 1×1 LEGO-stenen, krijg je geen perfecte bol. Je bol zal iets hoger zijn dan hij breed is, net als een 1×1-steen. Gelukkig is er ook een Plotz Ellipsoid Generator beschikbaar op dezelfde site en je kunt die gebruiken en de vorm van een 1×1 steen compenseren.
Voor de bol die ik bouwde met LEGO stenen, gebruikte ik Plotz om een ellipsoïde te maken met een breedte en diepte van 36 eenheden en een hoogte van 30 eenheden. Waarom heb ik een vorm gekozen die een beetje gedrongen is vergeleken met een perfecte bol? Let op dat de verhouding van hoogte tot breedte van de ellipsoïde 5/6 is, wat het omgekeerde is van de verhoudingen van een 1×1 LEGO steen (die een hoogte tot breedte verhouding heeft van 6/5). En dus wanneer we LEGO stenen gebruiken die hoger zijn dan ze breed zijn, worden de verhoudingen gelijk en eindigen we met een perfecte bol.

De bol ziet er goed uit, maar is een beetje blokkerig. Is er een manier om de rondingen gladder te maken, misschien door LEGO-platen te gebruiken die 1/3 zo hoog zijn als stenen? We gaan terug naar de Plotz Ellipsoid Generator en deze keer moeten de getallen die we gebruiken de vorm van een 1×1 LEGO-plaat weerspiegelen met een hoogte-breedteverhouding van 2/5. Ik gebruikte een hoogte van 50 eenheden en een breedte van 20 eenheden, wat ons een hoogte-breedteverhouding van 5/2 geeft. Op deze manier krijgen we een perfecte bol wanneer we de Minecraft-blokken vervangen door 1×1 LEGO-platen (indien nodig gecombineerd tot langere platen).
Als we deze bol van de zijkant bekijken, zien we een duidelijke verbetering in vergelijking met de eerdere bol. De rondingen zijn veel gladder dankzij de kleinere gradaties die worden bereikt door platen in plaats van stenen te gebruiken. Maar de beperkingen van deze aanpak worden duidelijk wanneer je de bol omdraait en er van bovenaf naar kijkt. Vanuit dit perspectief lijken de rondingen opnieuw blokkerig. Het blijkt dat het gebruik van platen om de bol te bouwen de rondingen alleen maar vloeiender maakt in een van de drie dimensies. Een ander nadeel van bollen die gebouwd zijn door stenen of platen te stapelen, is dat de onderkanten van de stenen en platen zichtbaar zijn als je naar de onderkant van de bol kijkt.

Is er een manier om vloeiendere rondingen te krijgen in alle 3 dimensies zonder dat die vervelende onderkanten van platen zichtbaar zijn? Als we alleen het bovenste deel van deze bol zouden kunnen nemen dat gladder is en het op de een of andere manier in alle 3 dimensies (alle 6 zijden) zouden kunnen gebruiken, zouden we een bol hebben die er rondom glad uitziet – klopt dat? Dat is precies het idee dat AFOL-extraordinaire Bruce Lowell in 2002 had. Zijn uitvinding bracht een soort revolutie teweeg in de constructie van ronde vormen (niet alleen bollen) met LEGO, waardoor hij de onderscheiding kreeg de enige AFOL (die ik ken) te zijn met een bouwtechniek die naar hem is vernoemd – de Lowell-bol!
6) Lowell-bollen
De laatste techniek die ik vandaag deel is de Lowell Sphere. Deze bestaat uit een SNOT-kubus (met noppen in alle richtingen) met 6 identieke gebogen panelen (gebouwd met LEGO-platen) bevestigd aan alle 6 zijden. Elk paneel is langer dan breed, waardoor de 6 panelen perfect in elkaar passen zonder zichtbare openingen. De originele bol van Bruce Lowell had een diameter van 6,8 noppen en een binnenkern die 4x4x4 noppen breed was. Maar in de jaren die volgden, heeft deze techniek een eigen leven gekregen en toepassingen gevonden in niet alleen bollen, maar ook in andere complexe sculpturen.

Afbeelding via LEGO Ideas
Hoewel de originele 6,8-stud brede bol vrij eenvoudig te achterhalen is, hoe pas je deze techniek toe om grotere bollen te bouwen? Een andere AFOL die een sleutelrol heeft gespeeld bij het toegankelijk maken van deze techniek voor iedereen is Bram Lambrecht. Hij ontwikkelde Bram's Sphere Generator waarmee je een Lowell Sphere kunt maken met elke diameter die je nodig hebt. Voer gewoon de diameter in (in stappen van 0,2 studs), pas een paar instellingen aan en je bent klaar om een Ldraw-bestand op te slaan dat kan worden geïmporteerd in Stud.io. Er is een optie om half-stud offsets (jumper plates) te gebruiken om meer details te krijgen, maar ik heb ontdekt dat dit niet praktisch is voor grotere bollen.
Een zeer nuttige instelling is "gebruik afwisselende laagkleuren" en met deze instelling geselecteerd, worden verschillende kleuren gebruikt voor de lagen platen die elk van de 6 identieke panelen vormen. Je vraagt je misschien af waarom dat nuttig is. Het Ldraw-bestand heeft submodellen voor de 6 panelen. Maar wanneer u een van deze submodellen vrijgeeft (degroepeert), zult u zien dat elk paneel volledig is opgebouwd uit 1×1-platen. Er is dus wat werk bij betrokken, laag voor laag en het vervangen van de 1×1-platen door grotere.
U moet de platen zo kiezen dat het hele paneel als één geheel bij elkaar blijft (door ervoor te zorgen dat de naden tussen de platen niet op één lijn liggen tussen opeenvolgende lagen). Het goede nieuws is dat u, zodra u aan een paneel hebt gewerkt, het weer kunt opslaan als een submodel en dat voor alle 6 zijden kunt gebruiken. Het Ldraw-bestand bevat ook niet de kern en dus zult u dat moeten bouwen als een SNOT-kubus met noppen in alle 6 richtingen (gewoonlijk is een handvol verbindingspunten voor elk van de 6 panelen voldoende).

Voor de ronde koepel van de Taj Mahal heb ik een Lowell-bol gemaakt met een diameter van 27,2 noppen. Deze bestaat uit een kern van 16x16x16 noppen en 6 gebogen panelen die elk 14 platen dik zijn (dus de diameter is 16 noppen + 28 platen, wat gelijk is aan 16 + 11,2 = 27,2 noppen). Het was duidelijk dat ik het onderste deel van de bol niet nodig had en dus moest ik het afkappen. Uiteindelijk heb ik het onderste paneel van de bol helemaal verwijderd en de hoogte van de kern met 2 noppen teruggebracht tot 14 noppen.
Ik moest ook de onderste delen van de gebogen panelen aan de 4 zijden bijsnijden (omdat de panelen op twee verschillende manieren zijn georiënteerd, moest ik twee varianten van de bijgesneden zijpanelen maken). Het onderste gedeelte van de koepel dat op de trommel rust, had uiteindelijk een diameter van 16 noppen + 22 platen = 24,8 noppen, wat heel dicht bij de buitendiameter van de trommel (25 noppen) lag.

Het concept van de Lowell Sphere kan worden uitgebreid naar andere vormen. Lsculpt, ook ontwikkeld door Bram Lambrecht, stelt je in staat om een 3D-model om te zetten in een LEGO-sculptuur die is gestructureerd als een Lowell Sphere met een SNOT-kern (dat is niet per se een kubus) die gebogen panelen heeft die in alle 3 dimensies zijn bevestigd. Hier is een hartsculptuur die ik digitaal heb gebouwd met Lsculpt.
Even afronden :-)
De technieken die ik heb opgesomd zijn slechts het topje van de ijsberg, om het zo maar te zeggen. Er zijn nog een aantal andere ingenieuze technieken die mensen hebben bedacht om ronde vormen te bouwen met LEGO. Hopelijk kan dit artikel je een goed startpunt geven voor je eigen verkenning van deze technieken (op Flickr en andere sites). Voel je vrij om opmerkingen te plaatsen over een specifieke techniek die je favoriet is (zelfs als ik die hier niet heb behandeld).
-

Investeren in LEGO... interessant of beter toch niet? (deel 1)
LEES MEER -

De LEGO Groep roept leveranciers op om te streven naar 0 uitstoot
LEES MEER -

Waarom heeft deze LEGO set 1138 Steentjes?
LEES MEER -

LEGO Fortnite Samurai Darth Vader???
LEES MEER -

-

Komt er een LEGO Snoopy
LEES MEER -

Drijvende zee otter
LEES MEER -

Komt er een LEGO set van Kuifje?
LEES MEER -

Fan van Downton Abbey? bouw het kasteel
LEES MEER
NIEUWSTE LEGO SETS
-
 Aanbieding
AanbiedingLEGO 3-in-1 dieren op wielen 10448 DUPLO
Normale prijs £27.00 GBPNormale prijs£32.00 GBPAanbiedingsprijs £27.00 GBPAanbieding -

 Aanbieding
AanbiedingLEGO Hopsy's kasteelspel 10450 DUPLO
Normale prijs £31.00 GBPNormale prijs£36.00 GBPAanbiedingsprijs £31.00 GBPAanbieding -
LEGO 3-in-1 dinosaurussen op wielen 10451 DUPLO
Normale prijs £54.00 GBPNormale prijs£63.00 GBPAanbiedingsprijs £54.00 GBPAanbieding -
LEGO McQueens bezoek aan Docs garage 10456 DUPLO
Normale prijs £24.00 GBPNormale prijs£27.00 GBPAanbiedingsprijs £24.00 GBPAanbieding -
LEGO De tuin en kas van Opa Big 10461 Peppa Pig
Normale prijs £61.00 GBPNormale prijs£72.00 GBPAanbiedingsprijs £61.00 GBPAanbieding -
LEGO De pikhouweelmijn 21277 Minecraft
Normale prijs £42.00 GBPNormale prijs -
 Aanbieding
AanbiedingLEGO De Enderman toren 21279 Minecraft
Normale prijs £76.00 GBPNormale prijs£90.00 GBPAanbiedingsprijs £76.00 GBPAanbieding -
LEGO Aston Martin Valkyrie 42208 Technic
Normale prijs £49.00 GBPNormale prijs -
 Aanbieding
AanbiedingLEGO Minnie's huisdierenhotel 43274 Disney
Normale prijs £31.00 GBPNormale prijs£36.00 GBPAanbiedingsprijs £31.00 GBPAanbieding -
LEGO Toy Story feesttrein en RC auto 43264 Disney
Normale prijs £31.00 GBPNormale prijs
VOOR JOU GESELECTEERD
-
LEGO Trevi Fontein 21062 Architecture
Normale prijs £122.00 GBPNormale prijs -
LEGO Piramide van Gizeh 21058 Architecture
Normale prijs £107.00 GBPNormale prijs -
LEGO Bouw je eigen Architecture bouwwerken met deze set Studio 21050 Architecture
Normale prijs £401.00 GBPNormale prijs -
LEGO De New York Skyline 21028 Architecture
Normale prijs £39.00 GBPNormale prijs -
LEGO Vrijheidsbeeld 21042 Architecture
Normale prijs £76.00 GBPNormale prijs -
LEGO Trafalgar Square London 21045 Architecture
Normale prijs £90.00 GBPNormale prijs -
LEGO New York Postkaart 40519 Creator
Normale prijs £17.00 GBPNormale prijs -

 Aanbieding
AanbiedingLEGO Kasteel Himeji 21060 Architecture
Normale prijs £122.00 GBPNormale prijs£143.00 GBPAanbiedingsprijs £122.00 GBPAanbieding -
LEGO Slot Neuschwanstein 21063 Architecture
Normale prijs £218.00 GBPNormale prijs -
LEGO Notre-Dame Kathedraal 21061 Architecture
Normale prijs £175.00 GBPNormale prijs
-

LEGO Avatar
LEGO Avatar: Duik in de wonderlijke wereld van Pandora! Bouw mee met...
-

LEGO Icons
Herbeleef je kindertijd met LEGO Icons sets, speciaal ontworpen voor nostalgische volwassenen....
-

LEGO Classic
Voor alle creatieve bouwers van 4 jaar en ouder! Met LEGO Classic...

























































