Wie baut man mit LEGO-Steinen etwas Rundes?
Wie baut man Formen mit quadratischen LEGO-Steinen, welche Berechnungstechniken sind dafür erforderlich und welche Rolle spielt Minecraft dabei?

Runde Formen aus quadratischen Steinen
LEGO ist kein geeignetes Baumaterial für den Bau runder Formen. Denn der Grundbaustein – ein 1x1-Stein – hat eine quadratische Grundfläche, auf einer LEGO-Grundplatte ist dagegen ein regelmäßiges quadratisches Raster aufgelegt.
Und doch gibt es viele wunderschöne LEGO-Kreationen mit runden Formen – alle Arten von Zylindern und sogar Kugeln.
Wir hatten viel Erfahrung mit dem Bauen dieser Formen mit LEGO, bis wir anfingen, an unserer eigenen Version des Taj Mahal zu arbeiten. Das Herzstück dieses berühmten Monuments, das zugleich eines der modernen Weltwunder ist, ist die gewaltige Kuppel, die auf einem zylindrischen Sockel steht, der „Trommel“ genannt wird (das ist ein echter Begriff aus der Architektur). Bei den Münzen, die an den vier Ecken des Sockels des Taj Mahal stehen, handelt es sich eigentlich auch um gestapelte Zylinder.


Vor einiger Zeit stießen wir auf das Modell des Taj Mahal, das vom verstorbenen Arthur Gugick angefertigt wurde. Dieses bemerkenswerte Modell war der Vorläufer des LEGO Creator Expert Sets 10189 und diente als zentrales Requisit im australischen Independent-Film „Taj“ (die Handlung dreht sich um einen Vater, der wieder Kontakt zu seiner entfremdeten Tochter aufnimmt, indem er mit ihr ein LEGO-Modell des Taj Mahal baut).
Wir wussten sofort, dass wir uns das Taj Mahal zu eigen machen wollten, wir waren noch nicht bereit dafür. Wir mussten noch viel lernen, bevor wir dieser Welt gerecht werden konnten.
So beeindruckend Sean Kenneys Modell des Empire State Buildings auch war, wir hatten keine großen Probleme, intuitiv zu verstehen, wie es gebaut wurde. Ein Wolkenkratzer wie das State Building besteht im Wesentlichen aus mehreren Stockwerken: Man muss lediglich einige Variationen des Stockwerkdesigns vornehmen und diese so oft wie nötig wiederholen, um das Ganze zu konstruieren. Interessanter wird es, wenn Sie die Spitze eines klassischen Wolkenkratzers bauen (wo sie sich zu einer Turmspitze verjüngt), Sie aber mit metrischen Wolkenkratzern konfrontiert werden (mit bemerkenswerten Ausnahmen, wie etwa der Krone des Chrysler Buildings).
Das Taj Mahal hingegen enthält mehrere organische Formen – Bögen und natürlich Koels – und ich wusste nichts über den Bau runder Formen mit LEGO

Während wir uns in den darauffolgenden Jahren intensiv mit dem Bau verschiedener Wolkenkratzermodelle beschäftigten, hatten wir das Taj Mahal stets im Hinterkopf.
Tatsächlich haben wir mehr als einmal mit dem Bau eines Modells des Taj Mahal begonnen, bevor wir aufgegeben haben, weil wir einfach herausfinden konnten, wie wir einen Bogen oder ein anderes Element in das Modell einbauen könnten.
Wir mussten auch alle verfügbaren Techniken zum Erstellen runder Formen mit LEGO gründlich erkunden; Wir haben das Internet nach allen Informationen zu diesem Thema durchforstet, die wir finden konnten. Bei jedem Schritt waren wir erstaunt und inspiriert von der unendlichen Kreativität der AFOL-Community und wir verwendeten auch einige von der Minecraft-Community entwickelte Tools.

Dass wir es dieses Mal geschafft haben, die Planung des Taj Mahal reibungslos voranzutreiben, ist wahrscheinlich ein Beweis für unsere Entwicklung als Bauunternehmer. Wir haben alle Techniken verwendet, die wir beim Modellieren von Wolkenkratzern gelernt haben – SNOT, Halbständerversatz, geneigte Wände usw. – sowie einige neue Techniken, die wir bei unserer Forschung kennengelernt haben.
Wir hoffen, dass dieser Artikel etwas Klarheit zum faszinierenden Thema des Bauens runder Formen mit LEGO bringen kann. Wir können nicht behaupten, eine der in diesem Artikel erwähnten Techniken erfunden zu haben, aber wir katalogisieren sie hier gerne zur zukünftigen Bezugnahme (mit Angabe der Erfinder, wenn möglich).
Den Kreis quadratisch machen
Was genau beinhaltet das Herstellen runder Formen aus LEGO? Der Titel dieses Beitrags bezieht sich auf die „Quadratur des Kreises“, ein uraltes mathematisches Problem, das die Menschen jahrhundertelang zu lösen versuchten, bis sich 1882 seine Unlösbarkeit herausstellte. Es ist jedoch möglich, nahe genug heranzukommen, indem man eine Näherung der Zahl π (Pi) verwendet.
In allen hier beschriebenen Techniken wird versucht, mit quadratischen oder rechteckigen Steinen bzw. Platten eine möglichst gute Annäherung an die runde Form zu erreichen.
Das Ergebnis ist nie perfekt und die Beschränkungen des LEGO-Mediums werden immer in den Unregelmäßigkeiten der Rundungen und Löcher sichtbar, die vor allem bei näherer Betrachtung des Modells erkennbar sind. Der Trick besteht jedoch darin, eine einigermaßen überzeugende Illusion einer runden Form zu erzeugen, zumindest wenn man das Modell aus der Ferne betrachtet.
1) Mit SNOT kleine Zylinder herstellen
Bei den Minaretten des Taj Mahal wollten wir uns nicht auf die kleine Auswahl an Zylinderteilen beschränken, die LEGO zur Verfügung stellt. Wir wollten einen anderen Weg ausprobieren, um Zylinder zu bauen, die auf jede gewünschte Höhe skaliert werden können. Mit der Verwendung von gekrümmten Neigungen und SNOT zum Erstellen abgerundeter Formen waren wir bereits vertraut (wir hatten diese Technik zum Bau der Krone unseres Modells des Chrysler Buildings verwendet). Mit der gleichen Technik können Zylinder mit unterschiedlichen Durchmessern hergestellt werden. Alle Zylinder im Bild unten können in zwei Bolzenhöhenintervallen gebaut werden.

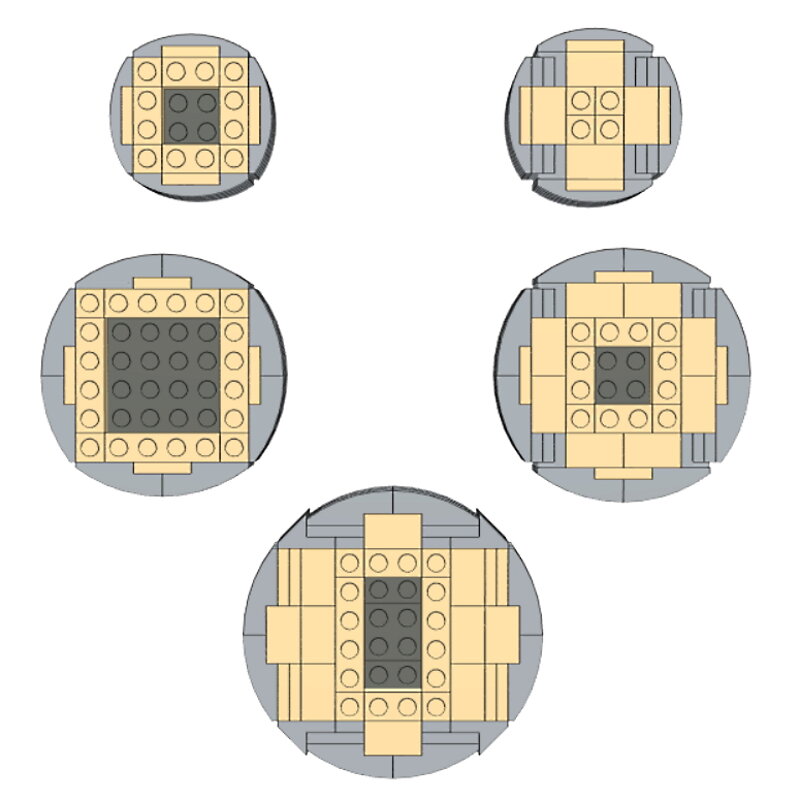
Der kleinste Zylinder war aufgrund meines Maßstabs genau richtig für die Minarette des Taj Mahal. Im Idealfall würden sich die Minarette nach oben hin verjüngen – so wie es beim echten Taj Mahal der Fall ist. Leider gab es keine einfache Möglichkeit, den Durchmesser des kleinsten Zylinders weiter zu reduzieren.
2) LEGO-Wände lassen sich biegen, um runde Formen zu bilden
Eine „brutale“ Methode, mit LEGO runde Wände zu konstruieren, besteht darin, gerade Wände zu bauen und diese dann zu einem Kreis zu biegen. Je länger die Wand ist, desto flexibler ist sie und desto leichter lässt sie sich zu einem vollen Kreis biegen. Die Anzahl der 12 Steine, die in jeder Reihe für eine einzelne runde Wand benötigt werden, liegt normalerweise bei etwa 72, plus oder minus ein paar Steine. Es sind allerdings auch Fälle bekannt, bei denen Rundwände mit deutlich weniger Platten pro Lage errichtet werden.
Schauen Sie sich die Arbeit von Jeff Sanders an, der auf das Biegen von Ziegeln spezialisiert ist. Er verfügt über ein beeindruckendes Portfolio an Kreationen, die er geschaffen hat, indem er Wände aus LEGO-Steinen nicht nur zu Kreisen, sondern auch in viele andere Formen gebogen hat.
Bitte beachten Sie, dass die meisten Techniken zum Biegen von Steinen strenggenommen „illegal“ sind, da Sie die LEGO-Elemente auf eine Weise verwenden, für die sie nicht vorgesehen sind, und sie unnötiger Belastung und möglicher Beschädigung aussetzen. Ein offensichtlicher Nachteil dieser Technik (abgesehen davon, dass sie illegal ist) ist die Tatsache, dass sie in der Stud.io-Software von BrickLink nicht digital repliziert werden kann.
Vor ein paar Jahren haben wir ein LEGO-Projekt gestartet, das anders war als alle anderen, an denen wir je gearbeitet hatten. Wir wollten eine runde Mosaikform mit Noppen nach oben herstellen. Wir haben uns unser eigenes Muster aus ineinander verschlungenen Schlangen ausgedacht und aus etwas mehr als 14.000 Platten dieses runde Ding gebaut, das wir uns gerne als eine Art Vase vorstellen (weil ein Mülleimer nicht sehr ansprechend ist). Das liegt irgendwo in einer Ecke unseres Kellers, weil wir noch immer keine gute Möglichkeit gefunden haben, es fertigzustellen und etwas Vorzeigbares daraus zu machen. Vorschläge sind natürlich willkommen!
3) Mischen von normalen Steinen mit runden 1×1-Steinen
Diese Technik verwendet denselben Ansatz wie oben – außer dass wir in unserer Wand runde 1×1-Ziegel (oder Platten) verwenden, um das Biegen einfacher (und legal!) zu machen. Wenn wir in unserer Mauer 1x3-Steine (1x2-Steine gehen auch) mit 1x1-Rundsteinen abwechseln, fungieren die Rundsteine bis zu einem gewissen Grad als Scharniere, sodass die Mauer sich zu einem Kreis krümmen kann. Dieses Verfahren ermöglicht den Bau runder Wände mit kleineren Durchmessern als mit der bisherigen Methode.
Der einzige Nachteil besteht darin, dass die Struktur der Wand aufgrund der 1x1 Rundsteine ungleichmäßig ist. Es ist möglich, die runden Steine durch Fliesen zu verbergen und so den Effekt einer echten Ziegelsteinmauer zu erzeugen (Credits gehen an Steve DeCraemer auf Flickr). Die 1x3-Steine werden hier durch 3 Scheinwerfer-Steine ersetzt, deren obere Noppen nach außen zeigen. Diese Scheinwerfersteine sind mit 1x3-Platten miteinander verbunden, während 1x4-Kacheln an der Vorderseite der kreisförmigen Mauer befestigt sind, was ihr das Aussehen einer Ziegelsteinmauer verleiht (was sich hervorragend für den Burgenbau eignet). 
4) Runde Wände mit Scharniersteinen und Platten
Wir haben gesehen, dass Scharnierstücke zum Erstellen von eckigen Wänden und verschiedenen Polygonen (Sechsecke, Achtecke usw.) sehr nützlich sein können. Je größer die Anzahl der Seiten eines regelmäßigen Polygons (bei dem alle Seiten gleich lang sind), desto näher kommt es einem Kreis. Diese Tatsache können wir uns zunutze machen, um mit Scharnierstücken runde Wände zu erstellen.
Ein Tutorial, das ich zu diesem Thema gefunden habe, war von Eggy Pop auf Flickr. Ich habe die in diesem Tutorial gezeigte kreisförmige Wand in Stud.io nachgebaut und dabei 14 1×4-Scharnierplatten verwendet, um den Kreis zu vervollständigen (der im Wesentlichen ein Polygon mit 28 Seiten mit der Breite von zwei Bolzen ist). Das Schöne an dieser speziellen runden Wand ist, dass der Durchmesser (18 Noppen innen, 20 Noppen außen) gemessen an der Anzahl der Noppen eine ganze Zahl ist. Wie Sie sehen, richten sich die Scharnierplatten an vier Seiten nach dem LEGO-Raster aus, sodass die runde Wand sicher an einer Basis befestigt werden kann.
Was also ist das Besondere an der Zahl 18? Mal sehen, ob wir das mithilfe der Mathematik herausfinden können. Unter der Annahme, dass die Innenseite der Wand annähernd die Form eines Kreises hat, wäre der Umfang gleich dem Durchmesser mal π (Pi) = 18 x 3,14 = 56,52 Bolzen. Teilen Sie das nun durch 4 (die Länge einer 1×4-Scharnierplatte) und Sie erhalten 14,13, was (für praktische Zwecke) nahe genug an der Ganzzahl 14 liegt – was zufällig der Anzahl der von uns verwendeten Scharnierplatten entspricht.
Verlassen Sie sich nicht darauf, dass dasselbe bei runden Wänden mit einem Innendurchmesser von beispielsweise 17 oder 19 Bolzen funktioniert. Welche anderen Nummern funktionieren? Die beiden Zahlen, die 18 am nächsten kommen und funktionieren, sind 14 und 23 (ich habe 23 für die Trommel in meinem Taj Mahal verwendet). Wie Sie auf den Bildern sehen können, funktionieren diese beiden Zahlen nicht so gut wie 18 und die Scharnierplatten auf nur zwei Seiten entsprechen dem LEGO-Raster (was normalerweise gut genug ist).
Können wir erklären, warum? Im Fall von 14 beträgt die Anzahl der erforderlichen Scharnierplatten (14 x 3,14) / 4, also ungefähr 11. Da die Anzahl der Scharnierplatten keine gerade Zahl ist, entsprechen die Scharnierplatten nicht auf allen 4 Seiten dem LEGO-Raster. Im Fall von 23 ist der Durchmesser selbst nicht gerade. Richtet man die Scharnierplatten auf einer Achse mit dem Gitter aus, wird die andere Achse um einen halben Balken verschoben (ggf. kann man auf den beiden anderen Seiten die Rundwand mit Überbrückungsplatten am Sockel befestigen).
Vorerst habe ich einfach eine normale Innenwand so nah wie möglich an der runden Wand gebaut und Käserampen, gebogene Rampen usw. mit SNOT an der Innenwand befestigt, um die Lücken so gut wie möglich zu füllen. Da die Trommel einen Außendurchmesser von 25 Bolzen hat und ich sie auf einer 24 x 24 Basis zentrieren musste, habe ich letztendlich Überbrückungsplatten verwendet. Ich brauchte außerdem Überbrückungsplatten, um die Kuppel (die aus einem 16x16-Bolzenkern besteht) oben auf der Trommel zu zentrieren.
Obwohl es ziemlich einfach ist, diese runden Wände mit echten Teilen zu bauen, wie macht man das in Stud.io? Mit dem Scharnierwerkzeug können Sie ein Teil auswählen und es um einen Scharnierpunkt drehen. In diesem Fall wäre das ausgewählte Stück die Hälfte der 1x4-Scharnierplatte. Wenn Sie bei aktiviertem Scharnierwerkzeug auf das Teil klicken, wird zunächst ein blauer Pfeil angezeigt. Sie können auf diesen blauen Pfeil klicken und ihn ziehen, um das Teil manuell zu drehen. Oder Sie klicken auf den blauen Pfeil, um ein weißes Textfeld zu öffnen, in dem Sie den genauen Winkel eingeben können, um den das Stück gedreht werden soll.
Bei runden Wänden ist darauf zu achten, dass alle Scharnierplatten genau im richtigen Maß gedreht sind, da sonst die beiden Enden der Wand nicht richtig ausgerichtet sind und der Kreis nicht geschlossen werden kann. Um den richtigen Winkel zu bestimmen, teilen Sie 360 durch die Anzahl der Seiten des Polygons, das Sie bauen. Beim ersten Kreis (Durchmesser 18 Bolzen) ist dies die Anzahl der Scharnierplatten mal 2 = 14 x 2 = 28. 360 geteilt durch 28 ergibt 12,85 Grad und diese Zahl müssen Sie in das Textfeld eingeben. Normalerweise wende ich diese Drehung auf eine Scharnierplatte an und kopiere und füge dann die Scharnierbaugruppe (beide Hälften zusammen) so oft ein, wie ich brauche.
5) Bauen Sie Kugeln, indem Sie normale Steine oder Platten stapeln
Um zu verstehen, wie Kugeln mit LEGO-Steinen gebaut werden, fand ich es hilfreich, zunächst einen Blick auf die Welt von Minecraft zu werfen. Es gibt einige Ähnlichkeiten zwischen Minecraft und LEGO, da beide Bausteine mit quadratischen Grundrissen verwenden, die auf einem quadratischen Raster angeordnet sind. Ein wichtiger Unterschied besteht darin, dass die Blöcke in Minecraft perfekte Würfel sind, während dies bei einem einfachen 1x1-LEGO-Stein nicht der Fall ist (er ist höher als breit). Mehr dazu später. Wie dem auch sei, in der Minecraft-Community stehen zahlreiche Ressourcen zum Bauen von Kugeln und anderen Formen mit Minecraft-Blöcken zur Verfügung, und ich habe mich gefragt, ob ich einige davon zum Bauen von LEGO-Kugeln verwenden könnte.
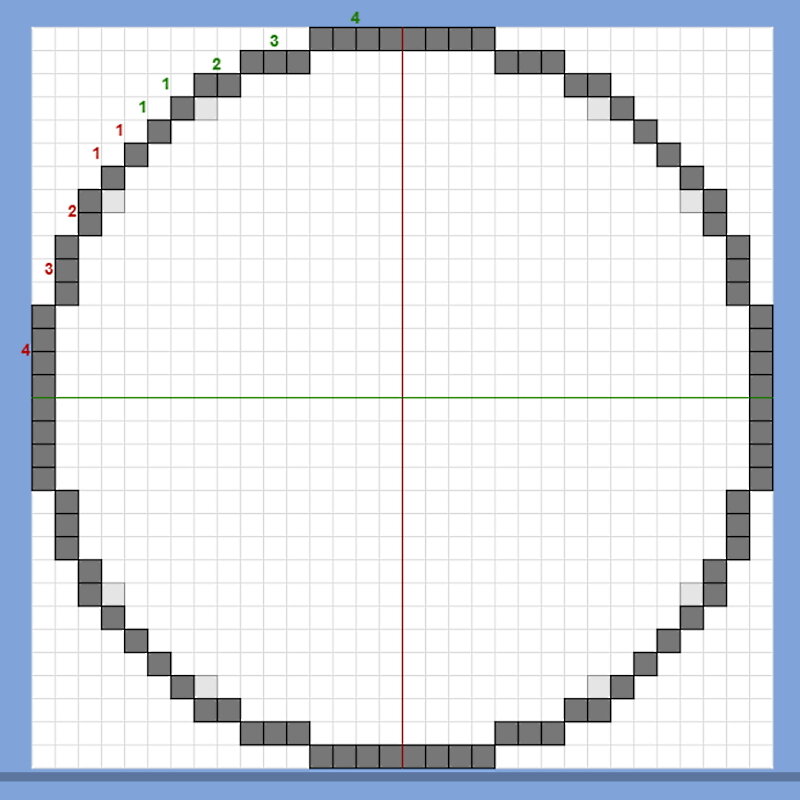
Bevor wir uns eine dreidimensionale Kugel ansehen, schauen wir uns einen einfachen Kreis in zwei Dimensionen an. Minecraft-Enthusiasten verwenden häufig ein sogenanntes Kreisdiagramm. Es zeigt die Platzierung von Blöcken (oder Pixeln) in einem quadratischen Raster, das am besten einem Kreis ähnelt. Das Diagramm zeigt Kreise mit unterschiedlichen Durchmessern. Wie Sie dem Diagramm entnehmen können, ist die Illusion der runden Form umso überzeugender, je größer der Durchmesser ist.

Minecraft-Kreisdiagramm
In der Minecraft-Welt, in der die Bausteine perfekte Würfel sind, können Sie auch einen der Kreise als Seite einer Kugel betrachten. Sie können sich jede Zeile im Diagramm als eine der Blockschichten der Kugel vorstellen, die Sie bauen. Sie beginnen also im Wesentlichen mit einer Schicht Blöcke in einem Kreis mit dem Durchmesser der Kugel, die Sie bauen möchten (das wäre der größte Kreis, den Sie brauchen). Anschließend stapeln Sie Schichten aus immer kleineren Kreisen (nach oben), bis Sie den kleinsten Kreis erreichen, den Sie benötigen. Wiederholen Sie dasselbe unten (machen Sie die Kreise nach unten hin kleiner), und Sie erhalten eine vollständige Kugel.
Natürlich kann es sehr aufwändig sein, dies alles manuell herauszufinden (selbst mithilfe eines Kreisdiagramms). Glücklicherweise kann ein Onlinetool (Plotz Sphere Generator) diesen Vorgang für Sie automatisieren. Geben Sie einfach den gewünschten Durchmesser ein und voilà, eine Kugel wird für Sie generiert (mit 3D- und 2D-Ansichten, die zeigen, wie die Kugel Schicht für Schicht aufgebaut wird).

Das klingt einfach, oder? Leider ist der Arbeitsaufwand deutlich größer, wenn man diese Kugel mit LEGO-Steinen bauen möchte. Erstens zeigt der Kugelgenerator nur Blöcke an, die 1x1 LEGO-Steinen entsprechen, aber Sie wissen, dass diese Steine nicht einfach gestapelt werden können, wie Sie in der 3D-Ansicht sehen. Sie müssen die 1x1 in längere Steine umwandeln, die eine ineinander greifende Struktur bilden, die gut zusammenhält.
Sie müssen außerdem die Wände der Kugel mindestens zwei Noppen tief machen, sodass jede nachfolgende Schicht (der Kreis wird immer kleiner, je weiter Sie sich von der mittleren Schicht entfernen) auf der Schicht direkt darunter aufliegen kann. Es gibt noch ein letztes Problem: Wenn Sie alle Blöcke in der Minecraft-Kugel durch 1x1-LEGO-Steine ersetzen, erhalten Sie keine perfekte Kugel. Ihre Kugel wird etwas höher als breit sein, ähnlich wie ein 1x1-Stein. Glücklicherweise steht auf derselben Site auch ein Plotz-Ellipsoid-Generator zur Verfügung, mit dem Sie die Form eines 1×1-Steins kompensieren können.
Für die Kugel, die ich aus LEGO-Steinen gebaut habe, habe ich mit Plotz ein Ellipsoid mit einer Breite und Tiefe von 36 Einheiten und einer Höhe von 30 Einheiten erstellt. Warum habe ich eine Form gewählt, die im Vergleich zu einer perfekten Kugel etwas gedrungen ist? Beachten Sie, dass das Verhältnis von Höhe zu Breite des Ellipsoids 5/6 beträgt, was dem Kehrwert der Proportionen eines 1×1-LEGO-Steins entspricht (dessen Verhältnis von Höhe zu Breite 6/5 beträgt). Wenn wir also LEGO-Steine verwenden, die höher als breit sind, gleichen sich die Proportionen aus und wir erhalten am Ende eine perfekte Kugel.

Die Kugel sieht gut aus, ist aber etwas blockig. Gibt es eine Möglichkeit, die Kurven zu glätten, vielleicht durch die Verwendung von LEGO-Platten, die 1/3 so hoch wie die Steine sind? Kehren wir zum Plotz-Ellipsoid-Generator zurück. Dieses Mal müssen die von uns verwendeten Zahlen die Form einer 1×1-LEGO-Platte mit einem Seitenverhältnis von 2/5 widerspiegeln. Ich habe eine Höhe von 50 Einheiten und eine Breite von 20 Einheiten verwendet, was ein Seitenverhältnis von 5/2 ergibt. So erhalten wir eine perfekte Kugel, wenn wir die Minecraft-Blöcke durch 1×1 LEGO-Platten (ggf. zu längeren Platten kombiniert) ersetzen.
Betrachtet man diese Kugel von der Seite, erkennt man eine deutliche Verbesserung gegenüber der vorherigen Kugel. Durch die Verwendung von Platten anstelle von Steinen sind die Kurven aufgrund der kleineren Abstufungen deutlich sanfter. Die Grenzen dieses Ansatzes werden jedoch deutlich, wenn man die Kugel umdreht und von oben betrachtet. Aus dieser Perspektive erscheinen die Kurven erneut blockförmig. Es stellt sich heraus, dass die Verwendung von Platten zum Bau der Kugel nur die Kurven in einer der drei Dimensionen glättet. Ein weiterer Nachteil von Kugeln, die aus aufeinander gestapelten Steinen oder Platten gebaut sind, besteht darin, dass die Unterseite der Steine und Platten sichtbar ist, wenn man auf die Unterseite der Kugel blickt.

Gibt es eine Möglichkeit, in allen drei Dimensionen glattere Kurven zu erhalten, ohne dass die störenden Plattenunterseiten sichtbar werden? Wenn wir einfach den oberen Teil dieser Kugel nehmen könnten, der glatter ist, und ihn irgendwie in allen 3 Dimensionen (allen 6 Seiten) verwenden könnten, hätten wir eine Kugel, die rundum glatt aussieht – ist das richtig? Genau diese Idee hatte AFOL-Experte Bruce Lowell im Jahr 2002. Seine Erfindung revolutionierte gewissermaßen die Konstruktion runder Formen (nicht nur Kugeln) mit LEGO und brachte ihm die Ehre ein, der einzige AFOL (soweit ich weiß) zu sein, nach dem eine Bautechnik benannt wurde – die Lowell-Kugel!
6) Lowell-Glühbirnen
Die letzte Technik, die ich heute vorstelle, ist die Lowell-Kugel. Es besteht aus einem SNOT-Würfel (mit Noppen in alle Richtungen) mit 6 identischen, gebogenen Platten (gebaut aus LEGO-Platten), die an allen 6 Seiten befestigt sind. Jedes Paneel ist länger als breit, sodass die 6 Paneele perfekt zusammenpassen, ohne dass sichtbare Lücken entstehen. Der Originalball von Bruce Lowell hatte einen Durchmesser von 6,8 Noppen und einen inneren Kern mit einer Breite von 4x4x4 Noppen. Doch in den darauffolgenden Jahren entwickelte sich diese Technik zu einem Eigenleben und fand nicht nur Anwendung bei Kugeln, sondern auch bei anderen komplexen Skulpturen.

Bild über LEGO Ideas
Während die ursprüngliche Kugel mit einer Breite von 6,8 Noppen relativ einfach zu replizieren ist, stellt sich die Frage, wie Sie diese Technik zum Bau größerer Kugeln anwenden können. Ein weiterer AFOL, der eine Schlüsselrolle dabei gespielt hat, diese Technologie für alle zugänglich zu machen, ist Bram Lambrecht. Er entwickelte Brams Kugelgenerator, mit dem Sie eine Lowell-Kugel mit jedem gewünschten Durchmesser herstellen können. Geben Sie einfach den Durchmesser ein (in 0,2-Bolzen-Schritten), passen Sie ein paar Einstellungen an und schon können Sie eine Ldraw-Datei speichern, die in Stud.io importiert werden kann. Es besteht die Möglichkeit, Halbbolzen-Offsets (Überbrückungsplatten) zu verwenden, um mehr Details zu erhalten, aber ich habe festgestellt, dass dies bei größeren Kugeln unpraktisch ist.
Eine sehr nützliche Einstellung ist „Abwechselnde Ebenenfarben verwenden“. Wenn diese Einstellung ausgewählt ist, werden für die Ebenen der Platten, aus denen die sechs identischen Paneele bestehen, unterschiedliche Farben verwendet. Sie fragen sich vielleicht, warum das nützlich ist. Die Ldraw-Datei enthält Untermodelle für die 6 Bedienfelder. Wenn Sie jedoch die Gruppierung eines dieser Untermodelle aufheben, sehen Sie, dass jedes Panel vollständig aus 1×1-Bretter besteht. Es ist also einige Arbeit erforderlich, die 1×1-Platten Schicht für Schicht durch größere zu ersetzen.
Sie sollten die Bretter so auswählen, dass die gesamte Platte als ein Stück zusammenhält (indem Sie darauf achten, dass die Nähte zwischen den Brettern zwischen den aufeinanderfolgenden Schichten nicht übereinander liegen). Die gute Nachricht ist, dass Sie ein Panel, nachdem Sie daran gearbeitet haben, erneut als Untermodell speichern und für alle 6 Seiten verwenden können. Die Ldraw-Datei enthält außerdem nicht den Kern, Sie müssen diesen also als SNOT-Würfel mit Bolzen in alle sechs Richtungen bauen (normalerweise reicht eine Handvoll Verbindungspunkte für jedes der sechs Paneele aus).

Für die runde Kuppel des Taj Mahal habe ich eine Lowell-Kugel mit einem Durchmesser von 27,2 Noppen angefertigt. Es besteht aus einem Kern aus 16 x 16 x 16 Noppen und 6 gebogenen Platten mit einer Dicke von jeweils 14 Platten (der Durchmesser beträgt also 16 Noppen + 28 Platten, was 16 + 11,2 = 27,2 Noppen ergibt). Es war klar, dass ich den unteren Teil der Glühbirne nicht brauchte, also musste ich ihn abschneiden. Schließlich habe ich die Bodenplatte der Kugel vollständig entfernt und die Höhe des Kerns um 2 Noppen auf 14 Noppen reduziert.
Ich musste auch die unteren Teile der gebogenen Paneele an den vier Seiten zuschneiden (da die Paneele in zwei verschiedene Richtungen ausgerichtet sind, musste ich zwei Varianten der zugeschnittenen Seitenpaneele herstellen). Der untere Teil der Kuppel, der auf der Trommel ruht, hatte schließlich einen Durchmesser von 16 Bolzen + 22 Platten = 24,8 Bolzen, was sehr nahe am Außendurchmesser der Trommel (25 Bolzen) lag.

Das Konzept der Lowell-Kugel kann auf andere Formen erweitert werden. Lsculpt, ebenfalls von Bram Lambrecht entwickelt, ermöglicht Ihnen die Umwandlung eines 3D-Modells in eine LEGO-Skulptur mit der Struktur einer Lowell-Kugel mit einem SNOT-Kern (der nicht notwendigerweise ein Würfel ist), an den in allen drei Dimensionen gekrümmte Platten angebracht sind. Hier ist eine Herzskulptur, die ich digital mit Lsculpt erstellt habe.
Nur zum Abschluss :-)
Die von mir aufgelisteten Techniken sind sozusagen nur die Spitze des Eisbergs. Es gibt noch eine Reihe weiterer raffinierter Techniken, die sich die Leute ausgedacht haben, um mit LEGO runde Formen zu bauen. Hoffentlich kann Ihnen dieser Artikel einen guten Ausgangspunkt für Ihre eigene Erkundung dieser Techniken (auf Flickr und anderen Websites) bieten. Kommentieren Sie gerne eine bestimmte Technik, die Ihnen am besten gefällt (auch wenn ich sie hier nicht behandelt habe).
-

In LEGO investieren... interessant oder lieber nicht? (Teil 1)
MEHR LESEN -

Die LEGO-Gruppe fordert Lieferanten auf, Null-Emissionen anzustreben
MEHR LESEN -

Warum besteht dieses LEGO-Set aus 1138 Steinen?
MEHR LESEN -

LEGO Fortnite Samurai Darth Vader???
MEHR LESEN -

-

Komt er een LEGO Snoopy
LEES MEER -

Drijvende zee otter
LEES MEER -

Komt er een LEGO set van Kuifje?
LEES MEER -

Fan van Downton Abbey? bouw het kasteel
LEES MEER
NEUESTE LEGO-SETS
-
LEGO 3-in-1 dieren op wielen 10448 DUPLO
Precio habitual CHF 29.00Precio habitualCHF 34.00Precio de oferta CHF 29.00Oferta -
LEGO Hopsy's kasteelspel 10450 DUPLO
Precio habitual CHF 33.00Precio habitualCHF 39.00Precio de oferta CHF 33.00Oferta -
LEGO 3-in-1 dinosaurussen op wielen 10451 DUPLO
Precio habitual CHF 58.00Precio habitualCHF 67.00Precio de oferta CHF 58.00Oferta -
LEGO McQueens bezoek aan Docs garage 10456 DUPLO
Precio habitual CHF 25.00Precio habitualCHF 29.00Precio de oferta CHF 25.00Oferta -
LEGO De tuin en kas van Opa Big 10461 Peppa Pig
Precio habitual CHF 65.00Precio habitualCHF 77.00Precio de oferta CHF 65.00Oferta -
LEGO De pikhouweelmijn 21277 Minecraft
Precio habitual CHF 45.00Precio habitual -
LEGO De Enderman toren 21279 Minecraft
Precio habitual CHF 82.00Precio habitualCHF 96.00Precio de oferta CHF 82.00Oferta -
LEGO Aston Martin Valkyrie 42208 Technic
Precio habitual CHF 52.00Precio habitualCHF 58.00Precio de oferta CHF 52.00Oferta -
LEGO Minnie's huisdierenhotel 43274 Disney
Precio habitual CHF 33.00Precio habitualCHF 39.00Precio de oferta CHF 33.00Oferta -
LEGO Toy Story feesttrein en RC auto 43264 Disney
Precio habitual CHF 33.00Precio habitual
FÜR SIE AUSGEWÄHLT
-
LEGO Trevi-Brunnen 21062 Architektur
Precio habitual CHF 130.00Precio habitual -
LEGO Pyramide von Gizeh 21058 Architektur
Precio habitual CHF 114.00Precio habitual -
LEGO Bauen Sie Ihre eigenen Architekturgebäude mit diesem Set Studio 21050 Architecture
Precio habitual CHF 431.00Precio habitual -
LEGO Die New York Skyline 21028 Architektur
Precio habitual CHF 42.00Precio habitual -
LEGO Freiheitsstatue 21042 Architektur
Precio habitual CHF 82.00Precio habitual -
LEGO Trafalgar Square London 21045 Architektur
Precio habitual CHF 96.00Precio habitual -
LEGO New York Postkarte 40519 Creator
Precio habitual CHF 18.00Precio habitual -
LEGO Himeji Castle 21060 Architektur
Precio habitual CHF 130.00Precio habitualCHF 153.00Precio de oferta CHF 130.00Oferta -
LEGO Slot Neuschwanstein 21063 Architecture
Precio habitual CHF 234.00Precio habitual -
LEGO Kathedrale Notre-Dame 21061 Architektur
Precio habitual CHF 188.00Precio habitual
-

LEGO-Avatar
LEGO Avatar: Tauchen Sie ein in die wunderbare Welt von Pandora! Bauen...
-

LEGO-Symbole
Erleben Sie Ihre Kindheit noch einmal mit LEGO Icons-Sets, die speziell für...
-

LEGO Classic
Für alle kreativen Baumeister ab 4 Jahren! Mit den LEGO Classic-Sets sind...

























































